The Truncated Cosine
This page will seek the Fourier Transform of the truncated cosine, which is given in Equation [1] and plotted in Figure 1.
This function is a cosine function that is windowed - that is, it is multiplied by the
box or rect function.
Figure 1. The Truncated Cosine given by Equation [1], for W=2.
Let's find the Fourier Transform of this function. To start, we can rewrite the function g(t)
as the product of two other functions:
To start, we can find the Fourier Transform of h(t) by recalling the
Fourier Transform of the Cosine Function, we can
determine H(f):
The Fourier Transform of the Box Function can be recalled, to determine K(f):
Now, the Fourier Transform of the multiplication of two function can be found by convolving their individual Fourier Transforms.
This is simply the modulation property of the Fourier Transform:
The convolution of H(f) and K(f) might seem difficult, but recall the property of
the dirac-delta impulse function:
Equation [6] is valid for all functions f(t), which will make Equation [5] simple to evaluate:
Now it's just algebra time. The last line can be rewritten as:
To further simplify the above, recall the trigonometric identities:
Hence, Term 1 = 0, and Term 2 can be simplified. The result is:
And there you have the result. The Fourier Transform G(f) is plotted in Figure 2:
Figure 2. The Fourier Transform of the Truncated Cosine for W=2
Fin.
Previous: The Shah Function
Fourier Pairs List
The Fourier Transform (Home)
This page on the Fourier Transform of the truncated cosine is copyrighted.
No portion can be reproduced except by permission from the author. Copyright thefouriertransform.com, 2010-2011.

[Equation 1]


[Equation 2]

[Equation 3]

[Equation 4]

[Equation 5]

[Equation 6]
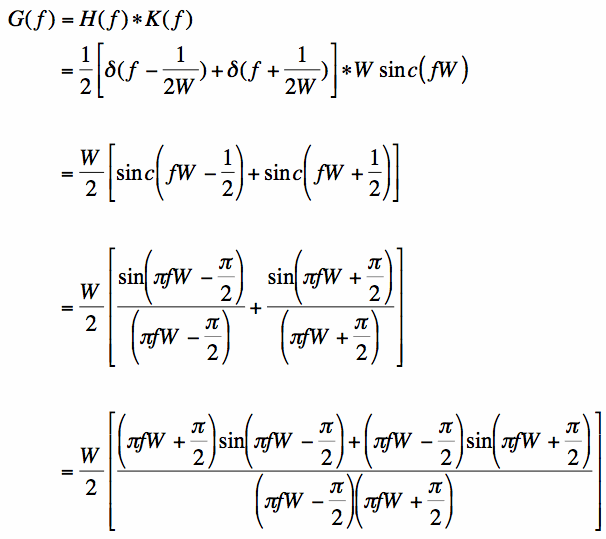


[Equation 7]

[Equation 8]

Next: Right-Sided Sinusoids