The Fourier Transform of the Box Function
On this page, the Fourier Transform for the box function, or square pulse, is given. This page is pretty much a rehash of the page in the
Fourier Transform theory section.
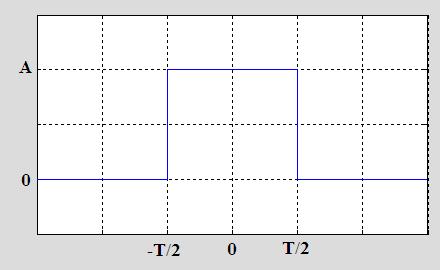
The box function is a square pulse, as shown in Figure 1:
Figure 1. The box function.
In Figure 1, the function g(t) has amplitude of A, and extends from t=-T/2 to t=T/2. For |t|>T/2, g(t)=0. We will
write the square pulse or box function as rect_T(t), indicating that the rectangle function is equal to 1 for a period of T (from -T/2 to +T/2) and 0 elsewhere:
Using the definition of the Fourier Transform
(Equation [1] on the intro page), the integral is
evaluated:
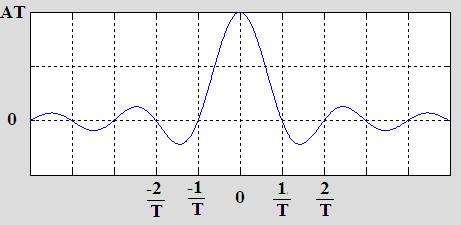
The solution, G(f), is often written as the sinc function, which is defined as:
[While sinc(0) isn't immediately apparent, using L'Hopitals rule or whatever special powers you have, you can show that sinc(0) = 1]
The Fourier Transform of g(t) is G(f),and is plotted in Figure 2 using the result of equation [2].
Figure 2. The sinc function is the Fourier Transform of the box function.
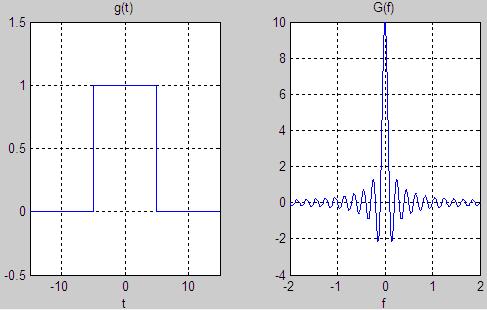
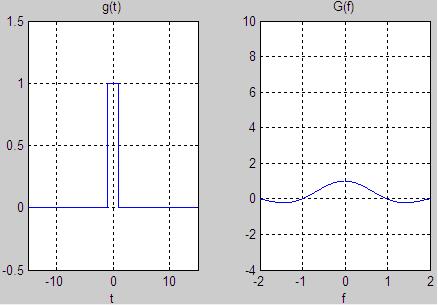
To learn some things about the Fourier Transform that will hold in general, consider the square pulses defined for T=10, and T=1.
These functions along with their Fourier Transforms are shown in Figures 3 and 4, for the amplitude A=1.
Figure 3. The Box Function with T=10, and its Fourier Transform.
Figure 4. The Box Function with T=1, and its Fourier Transform.
A fundamental lesson can be learned from Figures 3 and 4. From Figure 3, note that the wider square pulse produces a narrower, more constrained
spectrum (the Fourier Transform). From Figure 4, observe that the thinner square pulse produces a wider spectrum than in Figure 3.
This fact will hold in general: rapidly changing functions require more high frequency content (as in Figure 4). Functions that are moving more slowly in time
will have less high frequency energy (as in Figure 3).
In the next section, we'll look at the Fourier Transform of the triangle function.
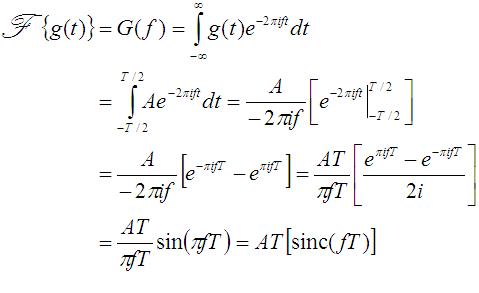 [1]
[1]
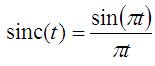
[Equation 2]
Next: The Triangle Function
Previous: Fourier Transform Pairs Table of Contents
The Fourier Transform (Home)