The Fourier Transform of the Triangle Function
Figure 1. The triangle function.
We'll give two methods of determining the Fourier Transform of the triangle function.
We can simply substitute equation [1] into the formula for the
definition of the Fourier Transform, then
crank through all the math, and then get the result. This is pretty tedious and not very fun, but here we go:
The Fourier Transform of the triangle function is the sinc function squared.
Now, you can go through and do that math yourself if you want. It's a complicated set of integration by parts, and then factoring the complex exponential
such that it can be rewritten as the sine function, and so on. It's an ugly solution, and not fun to do. Method 2, using
the convolution property, is much more elegant.
The convolution property was given on the Fourier Transform properties
page, and can be used to find Fourier Tranforms of functions. In some cases, as in this one, the property simplifies things.
If you've studied convolution, or you've sat down and thought about it, or you are very clever, you may know that the triangle function is
actually the convolution of the box function with itself. That is, let's simplify
box function on the previous page, g(t) such that the amplitude A=1 and T=1, then the box function is simply:
The triangle function can be mathematically expressed as the unit box function convolved with itself:
If you recall the convolution property of Fourier Transforms, we know that the Fourier Transform of the convolution of functions g1 and g2 is just the
product of Fourier Transform of the individual functions: (G1 times G2). Since we know the Fourier Transform of the box function is the sinc function,
and the triangle function is the convolution of the box function with the box function, then the Fourier Transform of the triangle function must be
the sinc function multiplied by the sinc function. That is:
So we arrive at the same solution as the brute-force calculus method, but we get there using a much simpler and more intelligent method.
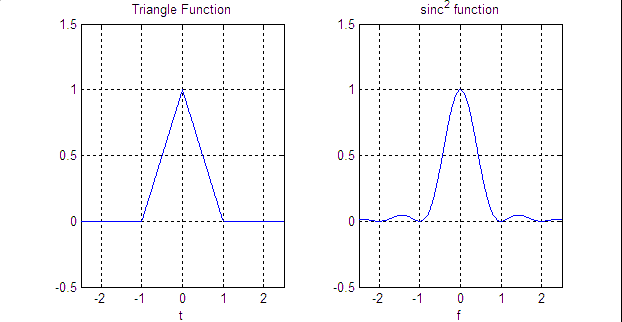
Either way, at the end of the day the Fourier Transform of the triangle function is the sinc function squared. This pair is shown in Figure 2.
Figure 2. The triangle function and its Fourier Transform the sinc squared function.
The Fourier Transform of the triangle function is derived on this page. The unit triangle function is given in Figure 1: 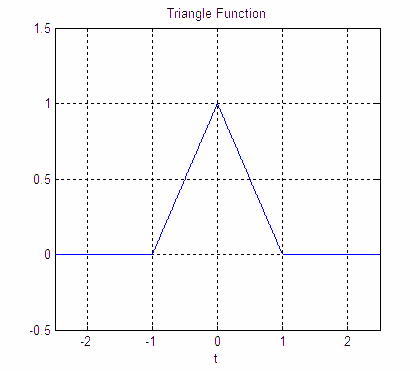
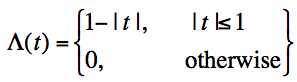
[Equation 1]
Method 1. Integration by Parts
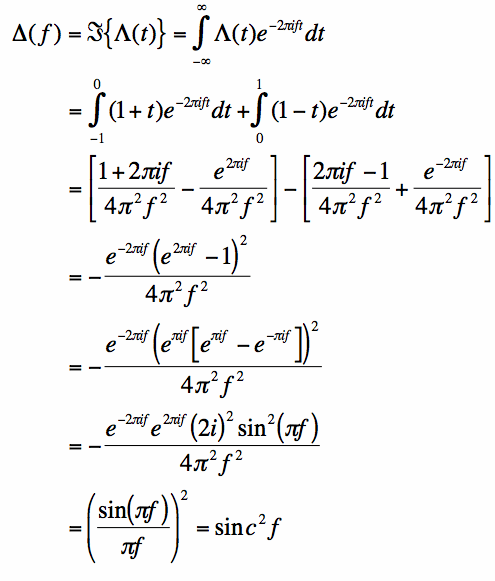
Method 2. Using the Convolution Property
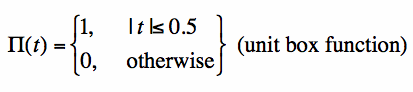
[Equation 2]
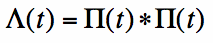
[Equation 3]
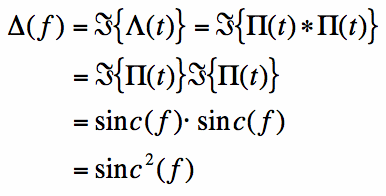
[Equation 4]
Next: Fourier Transform of the Gaussian
Previous: Fourier Transform of the Box (Square Pulse) Function
Fourier Transform Pairs (List)
The Fourier Transform (Home)