Fourier Transform Properties
In equation [1], c1 and c2 are any constants (real or complex numbers).
Equation [1] can be easily shown to be true via using the
definition of the Fourier Transform:
In the second step of [2], note that a simple variable substition u=t-a is used to evaluate the integral.
Equation [2] should make some intuitive sense. If the original function g(t) is shifted in time by a constant amount, it should have
the same magnitude of the spectrum, G(f). That is, a time delay doesn't cause the frequency content of G(f) to change at all. This should make
sense. Since the complex exponential always has a magnitude of 1, we see the time delay alters the phase of G(f) but not its magnitude.
Note that if we are taking the Fourier Transform of a spatial function (a function that varies with position, instead of time),
then our function g(x-a) would behave the same way, with x in place of t.
Let g(t) have Fourier Transform G(f). If the function g(t) is scaled in time by a non-zero constant c, it
is written g(ct). The resultant Fourier Transform will be given by:
The proof of Equation [3] can be found using the definition:
Now, if c is positive, the result is very simple:
If c is negative, the integration limits flip which introduces an extra minus sign:
Hence, you can see that for the general case of scaling with a real number c we get Equation [3].
(To see properties 2 and 3 in action together, this link uses the
scaling and shifting property on the Gaussian.)
The Fourier Transform of the derivative of g(t) is given by:
The convolution of two functions in time is defined by:
The Fourier Transform of the convolution of g(t) and h(t) [with corresponding Fourier Transforms G(f) and H(f)] is
given by:
A function is "modulated" by another function if they are multiplied in time. The Fourier Transform of the product is:
We've discussed how the Fourier Transform gives us a unique representation of the original underlying signal, g(t). That is, G(f) contains all the
information about g(t), just viewed in another manner. To further cement the equivalence, in this section we present Parseval's Identity for Fourier
Transforms.
Let g(t) have Fourier Transform G(f). Then the following equation is true:
The integral of the squared magnitude of a function is known as the energy of the function. For example, if g(t) represents the voltage across a
resistor, then the energy dissipated in the resistor will be proportional to the integral of the square of g(t). Equation [8] states that
the energy of g(t) is the same as the energy contained in G(f). This is a powerful result, and one that is central to understanding the equivalence
of functions and their Fourier Transforms.
Suppose g(t) has Fourier Transform G(f). Then we automatically know the Fourier Transform of
the function G(t):
This is known as the duality property of the Fourier Transform.
All of these properties can be proven via the
definition of the Fourier Transform. On the
next page, we'll look at the integration property of the Fourier Transform.
Next: The Integration Property
Previous: Fourier Transform of the Box Function
Fourier Transform Table of Contents
The Fourier Transform (Home)
On this page, we'll get to know our new friend the Fourier Transform a little better. Some simple properties of the Fourier Transform
will be presented with even simpler proofs. On the next page, a more comprehensive list of the Fourier Transform properties will be presented,
with less proofs: Linearity of Fourier Transform
First, the Fourier Transform is a linear transform. That is, let's say we have two functions g(t) and h(t), with Fourier Transforms
given by G(f) and H(f), respectively. Then the Fourier Transform of any linear combination of g and h can be easily found:
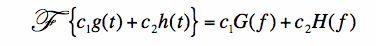
[Equation 1]
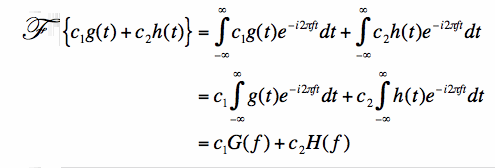
Shifts Property of the Fourier Transform
Another simple property of the Fourier Transform is the time shift: What is the Fourier Transform of g(t-a), where a is a real number?
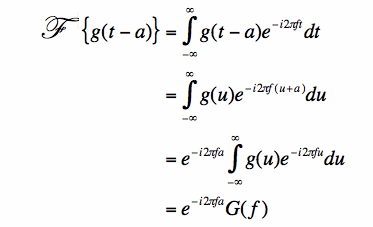
[Equation 2]
Scaling Property of the Fourier Transform
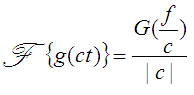
[Equation 3]
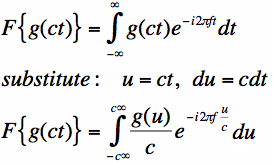
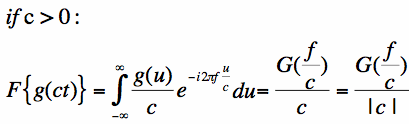
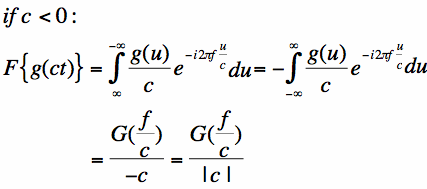
Derivative Property of the Fourier Transform (Differentiation)
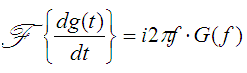
[Equation 4]
Convolution Property of the Fourier Transform
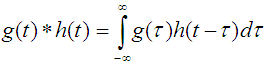
[Equation 5]
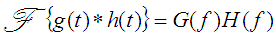
[Equation 6]
Modulation Property of the Fourier Transform
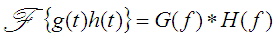
[Equation 7]
Parseval's Theorem
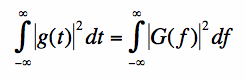
[Equation 8]
Duality
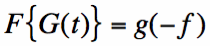
[Equation 9]