The Integration Property of the Fourier Transform
In words, equation [1] states that y at time t is equal to the integral of x() from minus infinity up to time t. Now, recall
the derivative property of the Fourier Transform for a function g(t):
Let's rewrite this Fourier property:
We can substitute h(t)=dg(t)/dt [i.e. h(t) is the time derivative of g(t)] into equation [3]:
Since g(t) is an arbitrary function, h(t) is as well and equation [4] gives a general result:
Equation [5] is "mostly" true. The reason it lacks completeness is that we used equation [3] to derive it -
and note that the derivative of g(t) removes any constant: that is, the derivative of g(t) is equal
to the derivative of the function g(t)+b, for any constant b. Because of this oversite, equation [5] is almost
correct. If the total integral of g(t) is 0, then equation [5] directly follows from equation [3], and we have:
If the total integral of g(t) is not zero, then there exists some constant c such that the total
integral of g(t)-c is zero:
That is, c is the "average value" of the function g(t), which is also often called the "dc term"
or the "constant term". Using some math and the
Fourier Transform of the impulse function,
we have the general formula for the Fourier Transform of the integral of a function:
The Dirac-Delta impulse function in [7] is explained here.
The integration property is used and the constant in [8] is utilized on
the Fourier Transform page for the unit step function, which should help clear
things up if the above is not clear.
Properties of the Fourier Transform
Fourier Transform Analysis (Table of Contents)
The Fourier Transform (Home)
On this page, we'll look at the integration property of the Fourier Transform. That is, if we have a function x(t) with
Fourier Transform X(f), then what is the Fourier Transform of the function y(t) given by the integral:
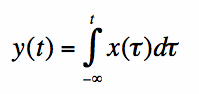
[Equation 1]
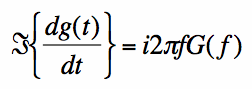
[Equation 2]
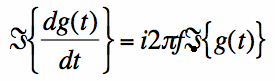
[Equation 3]
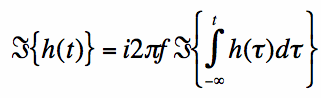
[Equation 4]
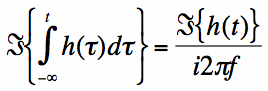
[Equation 5]
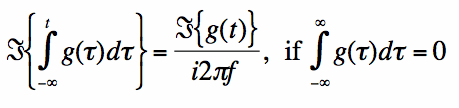
[Equation 6]
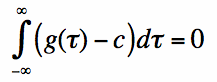
[Equation 7]
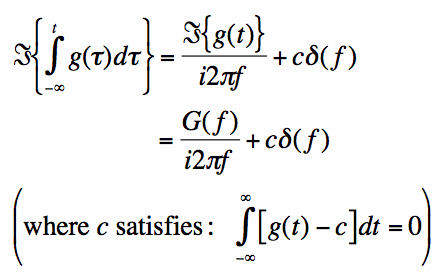
[Equation 8]
Next: Fourier Transform Pairs