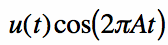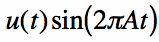The Fourier Transform of the 
Right-Sided Sine and Cosine Functions

The Fourier Transform can be found by noting the Fourier Transforms of the unit step and the cosine:

		[Equation 2]

		[Equation 3]

Using Equations [2] and [3] along with the modulation property of Fourier Transforms, we obtain the result:

		[Eq4]

The plot of the magnitude of the Fourier Transform of Equation [1] is given in Figure 2. Note that the vertical arrows represent dirac-delta functions.

Figure 2. Plot of Absolute Value of Fourier Transform of Right-Sided Cosine Function.

The Right-Sided Sine Function

The right-sided Sine function can be obtained in the same way. This function is mathematically written in Equation [5]:

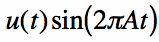		[Equation 5]

The plot of the right-sided Sine Function is given in Figure 3 for A=2:

Figure 3. Plot of Step Function times the Sine Function for A=2.

Recall the Fourier Transform of the Sine Function:

		[Equation 6]

And we can procede exactly as before to obtain the final result:

		[Eq7]

Equation 7 gives the Fourier Transform of the right-sided sine function. The absolute value of this function is plotted in Figure 4:

Figure 4. Plot of the Absolute Value of The Right-Sided Sine Function.