The Dirac-Delta Function - The Impulse
Using the definition of the Fourier transform, and the
sifting property of the dirac-delta, the Fourier Transform can be determined:
So, the Fourier transform of the shifted impulse is a complex exponential.
Note that if the impulse is centered at t=0, then
the Fourier transform is equal to 1 (i.e. a constant). This is a moment for reflection. The constant function, f(t)=1, is a function with no
variation - there is an infinite amount of energy, but it is all contained within the d.c. term. Since the fourier transform evaluated at f=0, G(0),
is the integral of the function. For f(t)=1, the integral is infinite, so it makes sense that the result should be infinite at f=0. And since
the function f(t) has no variation, it should have no frequency components, so the fourier transform should be zero everywhere f does not equal 0. This
last paragraph should be understood at an intuitive level.
The very useful Dirac-Delta Impulse functional has a simple Fourier Transform and
derivation. Particularly, we will look at the shifted impulse: 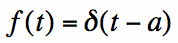 [1]
[1]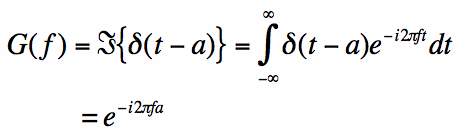 [2]
[2]
Next: The Complex Exponential