The Fourier Transform of the Complex Exponential
The complex exponential is actually a complex sinusoidal function. Recall Euler's identity:
Recall from the previous page on the dirac-delta impulse that the Fourier Transform of
the shifted impulse is the complex exponential:
If we know the above is true, then the inverse Fourier Transform of the complex exponential must be the impulse:
What we are interested in is the Fourier Transform of the complex exponential in equation [1], or:
The complex exponential function is common in applied mathematics. The basic form is written in Equation [1]: 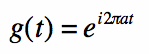 [1]
[1]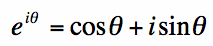 [2]
[2]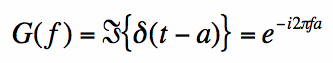 [3]
[3]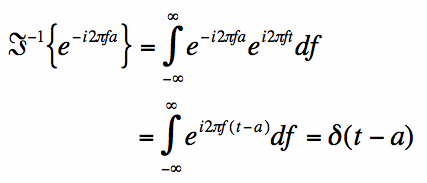 [4]
[4]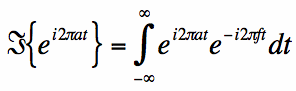 [5]
[5]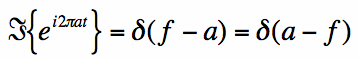 [6]
[6]
Next: Sinusoidal Functions - Sine and Cosine
Previous: The Dirac-Delta Impulse Function
Fourier Transform Pairs Table of Contents