The Fourier Transform of the Gaussian
The Gaussian curve (sometimes called the normal distribution) is the familiar bell shaped curve that arises all over mathematics, statistics, probability,
engineering, physics, etc. We will look at a simple version of the Gaussian, given by equation [1]:
The Gaussian is plotted in Figure 1:
Figure 1. The Gaussian Bell-Curve.
We will now evaluate the Fourier Transform of the Gaussian function in Figure 1. Let G(f) be the Fourier Transform of g(t), so that:
To resolve the integral, we'll have to get clever and use some differentiation and then differential equations. Take the derivative of both sides of
equation [2] with respect to f, so that:
Now we have this set up so that we can use integration by parts. That is, let
Recall the formula for integration by parts:
The uv term in equation [5] becomes zero, because the limits are evaluated from -infinity to +infinity, where
the product is zero. Using this fact and equations [3-5], we get:
This is a first order simple differential equation for G(f). The solution for this differential equation is given by:
All we need to do now to find G(f) is figure out what G(0) is. G(0) is simply the average value of g(t), because if you substitute f=0
into the equation for G(f), equation [2], the complex exponential term goes away (equation [8]). The integral in equation 8 has actually
an elegant solution, developed by Euler (the proof of which won't be given here), but the result is:
Hence, we have found the Fourier Transform of the gaussian g(t) given in equation [1]:
Equation [9] states that the Fourier Transform of the Gaussian is the Gaussian! The Fourier Transform operation returns
exactly what it started with. This is a very special result in Fourier Transform theory.
The Fourier Transform of a scaled and shifted Gaussian can be found
here.
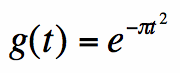 [1]
[1]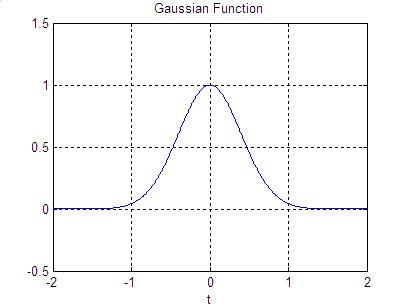
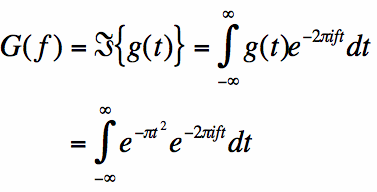 [2]
[2]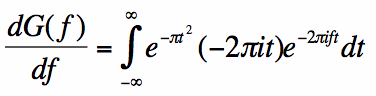 [3]
[3]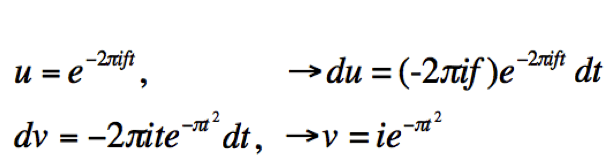 [4]
[4]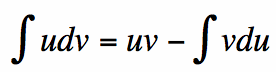 [5]
[5]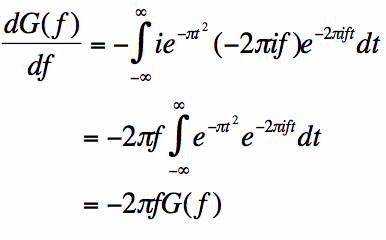 [6]
[6]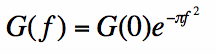 [7]
[7]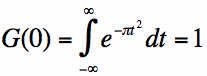 [8]
[8]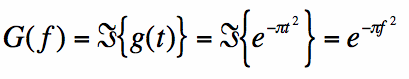 [9]
[9]
Next: The Dirac-Delta Impulse
Previous: The Triangle Function
Fourier Transform Pairs Table of Contents