Fourier Series Example - The Cosine Function
Figure 1. The Cosine Function.
First, we need to find the fundamental period, T. Since f(t) repeats itself 2 times from t=0 to t=1, the period
is T=0.5. We'll find the complex form of the Fourier Series, which is more useful in general than the entirely real Fourier Series
representation.
From equation [3] on the complex coefficients page,
To evaluate the integral simply, the cosine function can be rewritten (via Euler's identity) as:
Rewriting the integral with the above identity makes things easier. The above equation is substituted into equation [2], and
the result is:
Let's look at the first integral on the left in equation [4]. When n does not equal 1, note that the integral becomes zero:
The term in [brackets] is equation [5] is zero for all integer values of n. However, when n=1 the denominator is also zero, so the
equation is indeterminate. A simple way to evaluate the integral for n=1 is to plug in n=1 before the integration is done:
For the integral on the right in equation [4], the integral will be zero except when n=-1. Using the same type of analysis,
you can quickly figure out that:
Hence, all the coefficients are zero except for the n=1 and n=-1 terms. Finally, let's evaluate the infinite complex Fourier
Sum with the calculated coefficients and see that it gives f(t):
And we see that the Fourier Representation g(t) yields exactly what we were trying to reproduce, f(t). This might seem stupid,
but it will work for all reasonable periodic functions, which makes Fourier Series a very useful tool. In the next section, we'll
look at a more complicated example, the saw function.
To illustrate determining the Fourier Coefficients, let's look at a simple example. The cosine function, f(t), is shown
in Figure 1: 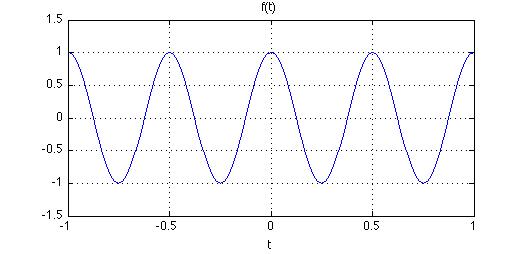
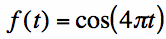 [1]
[1]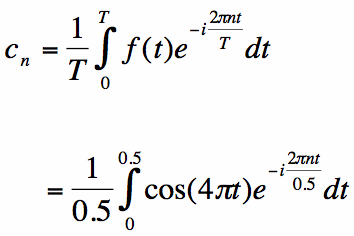 [2]
[2]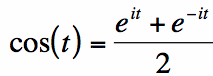 [3]
[3]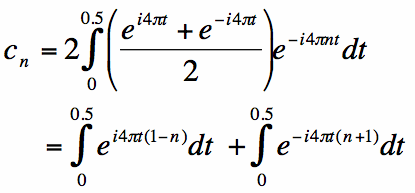 [4]
[4]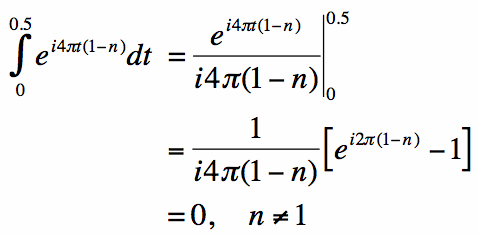 [5]
[5]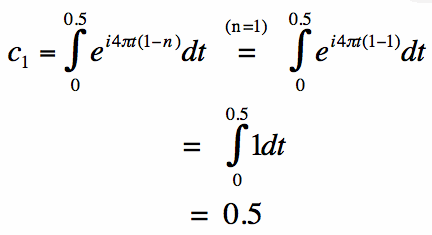 [6]
[6]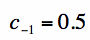 [7]
[7]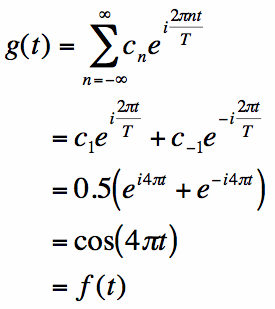 [8]
[8]
Previous: The Complex Fourier Coefficients
Fourier Series Homepage
The Fourier Transform (Home)