Fourier Series Example - The Saw Function
Figure 1. The Saw Function.
The determination of the Fourier Coefficients is fairly simple. The integral below in Equation [2]
can be determined with integration by parts, or a table look up, or whatever method you choose:
The above integral is simplified using the fact:
Observe from Equation [2] that nth term is the complex conjugate of the -nth term, so the resultant complex Fourier sum
will be real. To illustrate that the above coefficients do reproduce the saw function, the coefficients from Equation [2]
are plugged into Equation [1] from the Complex Fourier Coefficients page.
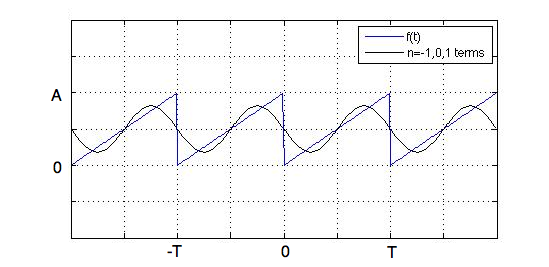
The n=-1, 0, 1 terms give the following function [superimposed on the original f(t) ]:
Figure 2. The Saw Function with 3 Fourier Coefficients (n=-1,0,1).
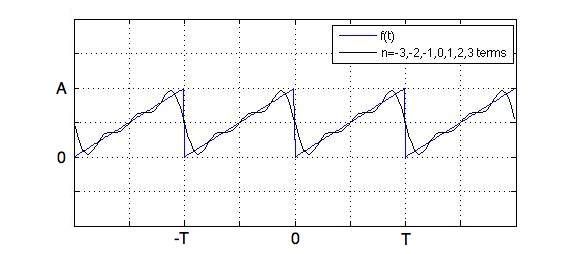
Figure 3. The Saw Function with 7 Fourier Coefficients (n=-1,0,1).
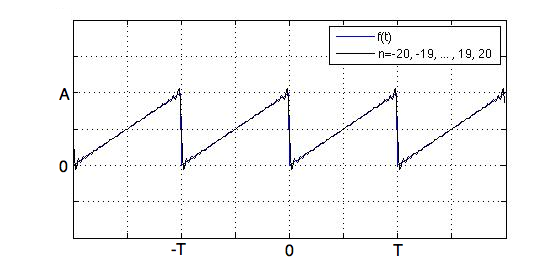
Figure 4. The Saw Function with 41 Fourier Coefficients (n=-20,-19,...19,20).
In the next section, we'll look at a complicated function that cannot be easily evaluated analytically (if at all), and determine
the Fourier Series numerically.
On this page, we'll look at another example of finding the Fourier Series - this time on the saw function.
The saw function, f(t), is illustrated in Figure 1: 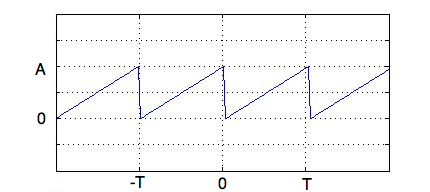

[Equation 1]

[Equation 2]

[Equation 3]
Next: Numerical Evaluation of Fourier Series of a Complicated Function
Previous: Fourier Series Example - The Cosine Function
Fourier Series (Table of Contents)
The Fourier Transform (Home)