Fourier Series - Complex Coefficients
Again, we want to rewrite a periodic function f(t) with period T with the infinite sum of sinusoidal functions. In this case,
we will use the complex exponential function as the basis. That is, we want to find the coefficients cn in the following formula:
Note that the complex exponential is the sum of sinusoidal functions, since the following identity can be proven:
If you are unfamiliar with the rules of complex math (a neccessity for understanding the Fourier Transform),
review the complex math tutorial page.
From Equation [1], the unknown Fourier coefficients are now the cn, where n is an integer between negative infinity and
positive infinity. The optimal value for cn are:
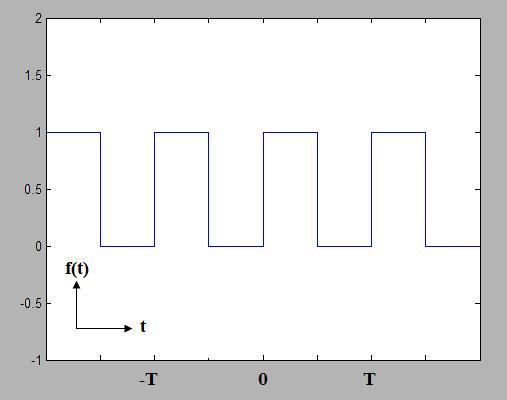
Recall the square function:
Figure 1. A periodic square waveform.
Note that the Fourier coefficients are complex numbers, even though the series in Equation [1], evaluated with the coefficients in Equation
[4], result in a real function. If the following condition (equation [5]) is true, then the resultant function g(t) will be entirely real:
In equation [5], the * represents the complex conjugate.
As an exercise, it would be enlightening to show that the results from the previous page on real Fourier coefficients,
with the am, bn values, yield the exact same function as the complex version with the cn values given on this page. This can be shown
with the help of the following identities, which should be memorized (along with Equation [2]):
On the next page, we'll look at some more examples.
The previous page on Fourier Series used only real numbers. In engineering, physics and many applied fields, using complex numbers
makes things easier to understand and more mathematically elegant. On this page, we'll redo the previous analysis using the complex
form of the Fourier Series.
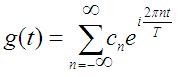
[Equation 1]
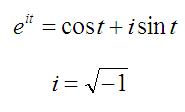
[Equation 2]
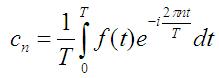
[Equation 3]
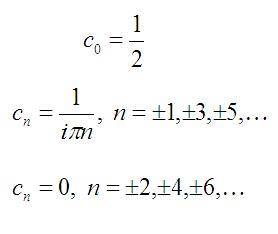
[Equation 4]
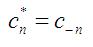
[Equation 5]
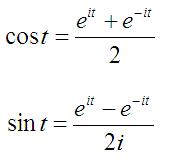
[Equation 6]
Next: Fourier Series Representation of the Cosine Function
Previous: Real (non-complex) Fourier Coefficients
Fourier Series (Main)
The Fourier Transform (Home)