Fourier Series - The Fourier Coefficients
We want to approximate a periodic function f(t), with fundamental period T, with the Fourier Series:
What are the optimal Fourier coefficients (a_m, b_n) of equation [1]? Let's start by looking at a one term approximation of the above:
Here we have a one-term approximation of the function. What is the best value for a0 that we can choose in this
case? Without proof (which will come later), the optimal value is:
How do we get this? Well, to answer intuitively, the integral of the function over the period is a formal mathematical
way of writing "the average value". So the first term in the Fourier series is a constant, and it is the average value
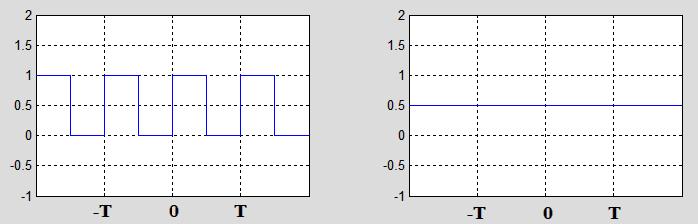
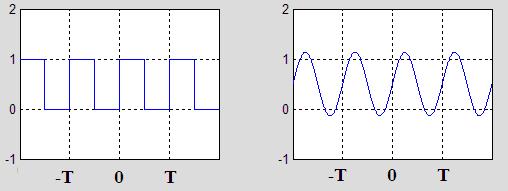
of the function. For the square wave of Figure 1 on the previous page, the average value is
0.5, and the one term expansion along with the function is shown in Figure 2:
Figure 2. The square waveform and the one term (constant) expansion.
What is the optimal value of b1? Intuitively, we want to know how correlated the function f(t) is with
sin(2*pi*t/T). In a sense, we want to correlate the function f(t) and this basis sine function. It turns out
the optimal value for b1 is given by:
This is the mathematical way of writing the correlation between two functions over the interval [0, T] (the derivation for the factor of 2 will
be shown later). Working through
the math of the above equation, the optimal value
for b1 is:
The first two terms from equation [4], evaluated with the optimal values for a0 and b1 now add together to produce:
Figure 3. The square waveform and the two term expansion.
Instead of going term by term, let's give the optimal coefficients for all am and bn:
All of these represent the correlation of the function f(t) with the basis sine and cosine functions.
For the specific square-wave f(t) of Figure 1, the optimal values come out to be:
Note that all of the a_m values (except a0) turn out to be zero. The simple reason for this
can be found by looking at the function
g(t)=f(t)-a0 [note: g(t) is the square wave with the constant offset removed so that the average of the function is zero]. It
turns out that g(t)
is an odd function, and the cosine functions are all even function
(click the links for the definition of even and odd functions). Hence, all the values a1, a2, ... do not contribute to g(t) [or f(t)],
so must be zero.
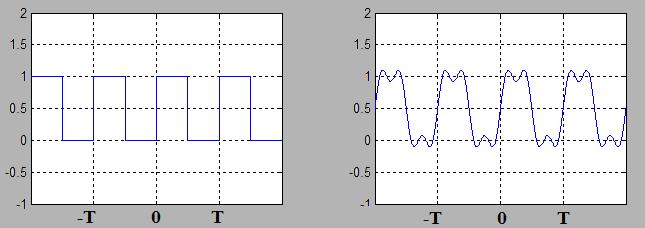
The first three non-zero term expansion (a0, b1, b3) is given in Figure 4:
Figure 4. The square waveform and the three term expansion.
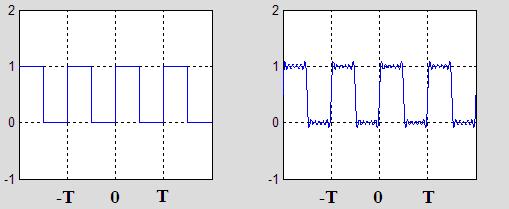
It looks like the whole Fourier Series concept is working. Here is a 7-term expansion (a0, b1, b3, b5, b7, b9, b11):
Figure 5. The square waveform and the seven term expansion.
The most important equation of this page is Equation 7 - the formulas for the Fourier Series coefficients.
These equations give the optimal values for any periodic function.
The main takeaway point from this page is to understand that any periodic function (it should be somewhat continuous) can be represented
by the sum of sinusoidal functions, each with a frequency some integer multiple of the fundamental period (T).
In the next section, we'll look at the complex form of the Fourier Series.
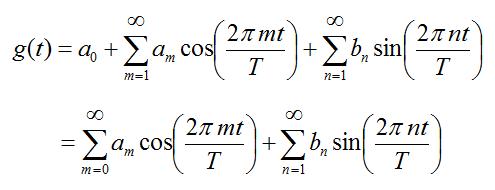
[Equation 1]
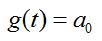
[Equation 2]
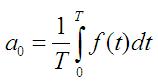
[Equation 3]
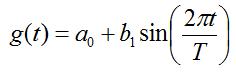
[Equation 4]
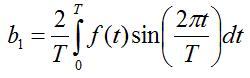
[Equation 5]
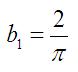
[Equation 6]
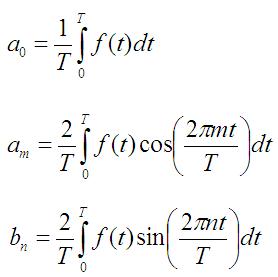
*[Equation 7]*
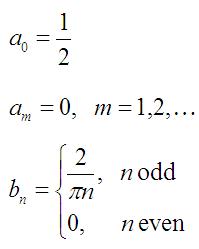
Next: The Complex Fourier Series Coefficients
Previous: Introduction to the Fourier Series
Fourier Series (Home)
The Fourier Transform (Home)