Fourier Series Application: Electric Circuits
Figure 1. A series R-C circuit.
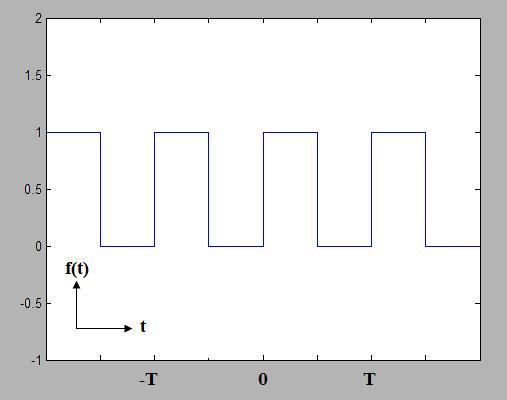
The source voltage Vs(t) will be a periodic square wave shown in Figure 1. The Fourier Series coefficients for this function
have already been found on the complex coefficients page.
Figure 2. A periodic square waveform.
The output voltage can be easily found with some application of Ohm's Law (V=I*Z):
From equation [2], we see that the output voltage can be easily calculated when the source voltage Vs is sinusoidal.
The question now is: how can we calculate the output voltage, Vo(t), when the input is not a sinusoidal function, but rather
any periodic function f(t)?
If you don't think the answer has something to do with Fourier Series, you probably need to work on your reading comprehension skills.
It just so happens that we know that any periodic function IS the sum of sinusoidal functions. And we know how to solve the circuit of
Figure 1 for any sinusoidal input. Finally, electric circuits are simple linear systems: this means that if an input voltage V1 produces
an output X1, and an input voltage V2 produces an output X2, then when the input V1+V2 is applied, the output is X1+X2.
The facts in the proceeding paragraph mean that with Fourier Series, the solution is very simple. We rewrite the square wave in terms
of a sum of sinusoidal functions, calculate the output via each one, and then sum up the solutions for each sinusoidal component.
To do this, let's choose a random component of the Fourier Series, say the nth component, corresponding to coefficient cn. This is
the coefficient that multiplies the complex exponential, with frequency given by f=n/T:
Using equation [3] in equation [2], the output voltage
for just this sinusoid (or complex exponential, they are basically the same), is:
In equation [4], note that the frequency f has been substituted with n/T, because that is the frequency of the corresponding
complex exponential that the cn multiplies. The cn values were already calculated on
the square wave page.
Since the electric circuit is linear, the total output voltage is given by the sum of all the components of the waveform:
When n=0, then f=0, so the output voltage is easily found from equation [2]. In this case, the output and input are equivalent, so that constant (non-varying)
term passes directly to the output.
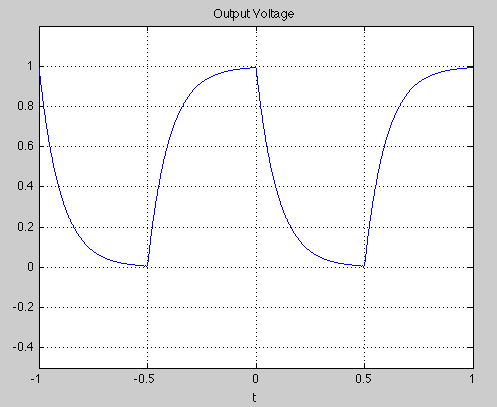
The output or solution voltage for R=1 Ohm, C=0.1 Farads, T=1s, is given in Figure 3:
Figure 3. Output Voltage, Vo(t).
This is the power of the Fourier Series. Many, many problems in engineering and physics can be solved analytically for the case of a
pure sinusoid input function. By using Fourier Series, the solution for all periodic functions can be quickly found. Hence, Fourier Series
is a very useful tool.
On this page, an the Fourier Series is applied to a real world problem: determining the solution for an electric circuit. Particularly,
we will look at the circuit shown in Figure 1: 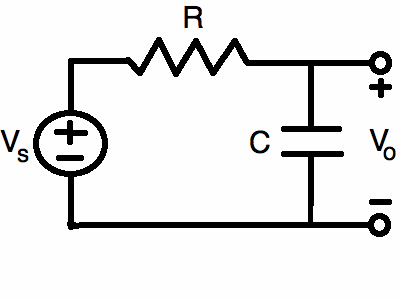
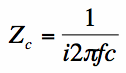
[Equation 1]
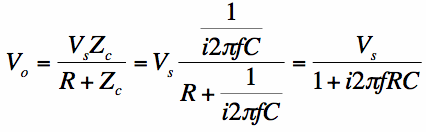
[Equation 2]
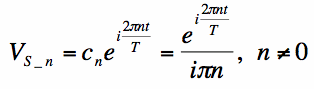
[Equation 3]
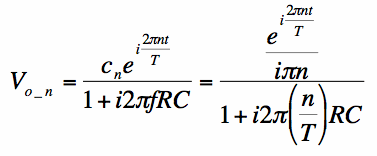
[Equation 4]
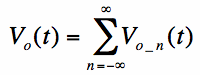
[Equation 5]
Previous: Derivation of Fourier Series Coefficients
Fourier Series Table of Contents
The Fourier Transform (Home)