Derivation of Complex Fourier Series Coefficients
The proof is fairly simple, assuming the Fourier Series g(t) does in fact converge to the original periodic function f(t). Assuming
the periodic function f(t), with fundamnetal period T, has a Fourier Series representation (it always does for any real world periodic
waveform). Then the following equation is true:
The goal is to determine the values for the cn in equation [2]. This can be done by multiplying both sides
of [2] with exp(-i*2*pi*m*t/T), and then integrating the product from t=[0,T]. The result will be the optimal solution
for cm, where m represent any integer.
To see this in action, let m be any integer, and multiply equation [2] by the complex exponential:
Now integrate both sides of equation [3] with respect to t from [0, T]:
In equation [4], the order of summation and integration was swapped, which is proper because both operators are linear.
The formal proof that infinite sums and integration can change their order is the life's work of some dead mathematician somewhere.
Finally, in the last step of [4], the constant cn can be pulled outside the integral, since it is just a constant.
Continuing, the integral of [4] can be easily evaluated. When n does not equal m, the integral is always zero.
When n=m, the integral will equal T:
Key point: As a result, the infinite sum only yields one non-zero term. Using equation [5] in equation [4], we get:
The integration gives zero for all terms except the mth term. As a result, equation [6] yields the solution for
cm: which is equivalent to equation [1].
In the next section, we'll look at applying the Fourier Series math to solving electric circuits.
On this page, we'll look at deriving where the formula for the Fourier Series coefficients come from. Namely, we look at the derivation
of this equation:
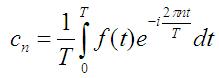
[Equation 1]
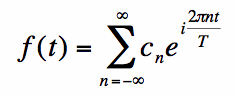
[Equation 2]
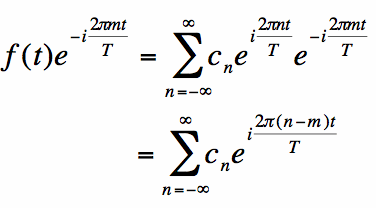
[Equation 3]
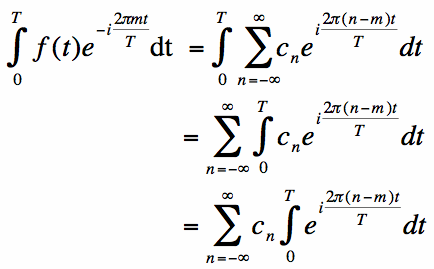
[Equation 4]
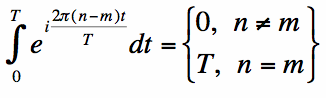
[Equation 5]
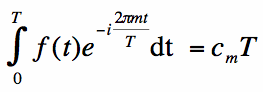
[Equation 6]
Next: An Application: Electric Circuits
Previous: Mean Squared Error
Fourier Series Homepage
The Fourier Transform (Home)