The Fourier Transform the Inverted Polynomial 1/(1+t^2)
On this page we seek the Fourier Transform for the inverted polynomial g(t):
The Fourier Transform is easily found, since we already know the
Fourier Transform for the two sided decaying exponential.
By using some simple properties, mainly the
scaling property of the Fourier Transform,
and the
duality relationship among Fourier Transforms.
Hence, we can obtain (proof not shown, that's for you!) the result [G(f)]:
What I think is cool about this Fourier Transform, is that if we recall the following indefinite integral:
We can compute the intergral from -infinity to +infinity using our Fourier Transform, and show that it
matches up perfectly with the indefinite integral result:
I like when everything works out, so I wanted to share that result in Equation [4] with you. Note that G(f)
is the result from Equation [2].
The Fourier Transform (Home)
This page on the Fourier Transform pair is copyrighted. No portion can be reproduced except by permission of the author.
Copyright www.thefouriertransform.com, 2010-2011, 2015.
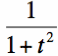
[Equation 1]
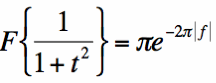
[Equation 2]

[Equation 3]
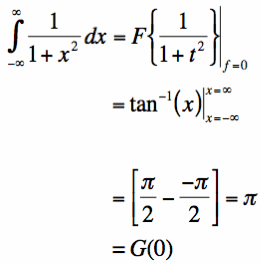
[Equation 4]
Fourier Transform Pairs (Table)