1- and 2-Sided Decaying Exponential
The decaying exponential function arises often in engineering and physical analysis of systems, in which
the magnitude of a function dies off over time. Examples include the voltage across a capacitor as a function
of time when a resistor is present, and from information theory, the expected amount of money you have left after
optimal gambling in a casino with non-favorable odds.
The one-sided (or right-sided) decaying exponential is given in Equation [1], and plotted in Figure 1.
Figure 1. Plot of Equation [1], the right-sided decaying exponential, for |a|=1.
Note that in Equation [1], and throughout this page, we use |a|, because this parameter must be positive,
or the Fourier Transform will diverge (and therefore not exist). The Fourier Transform for the right-sided exponential can be found from the Fourier Transform definition:
The left-sided decaying exponential is described by equation [3] and is plotted in Figure 2:
Figure 2. Plot of Equation [3], the left-sided decaying exponential, for |a|=1.
The Fourier Transform for the left-sided decaying exponential can be found exactly as done for the right-sided
in equation [2], giving:
The two-sided decaying exponential is given in equation [5], and plotted in Figure 3:
Figure 3. Plot of Equation [5], the two-sided decaying exponential, for |a|=1.
Note that k(t) = f(t) + g(t). Hence, the Fourier Transform can be easily found with
the linearity property:
That wraps up the study of the decaying exponential. Give yourselves a round of applause.
Right-Sided Decaying Exponentials
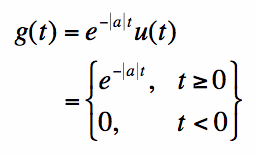 [1]
[1]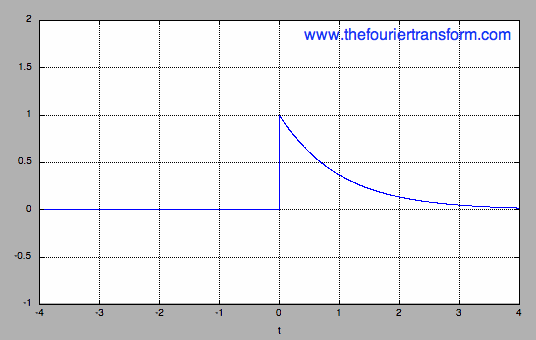
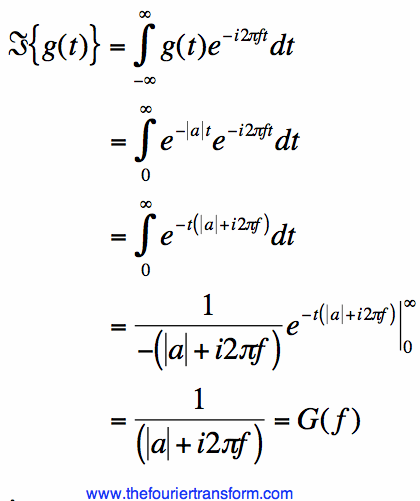 [2]
[2] Left-Sided Decaying Exponentials
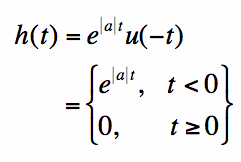 [3]
[3]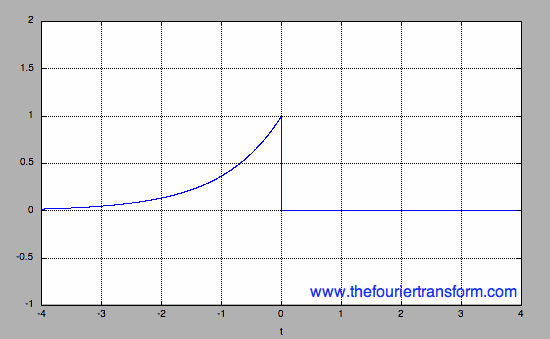
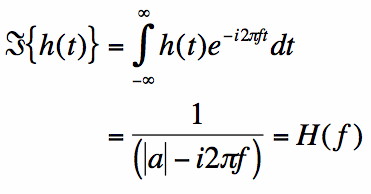 [4]
[4] Two-Sided Decaying Exponentials
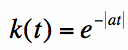 [5]
[5]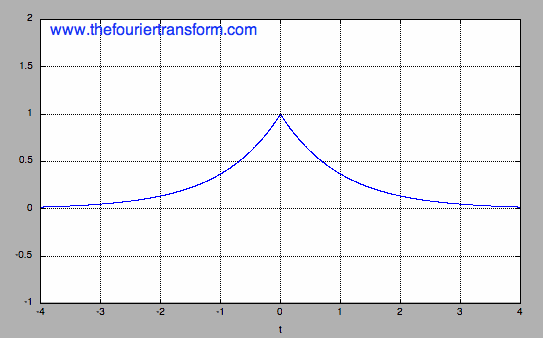
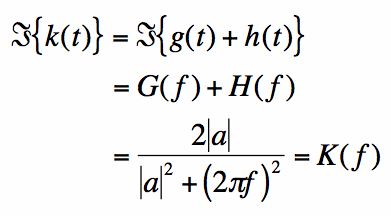 [6]
[6]
Next: The Shah Function