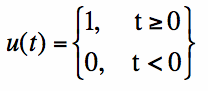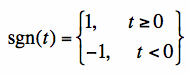The Step Function and the Signum Function
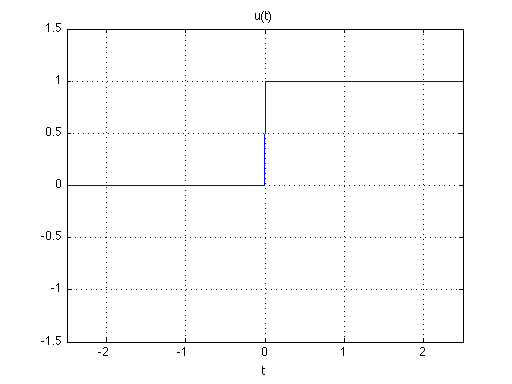
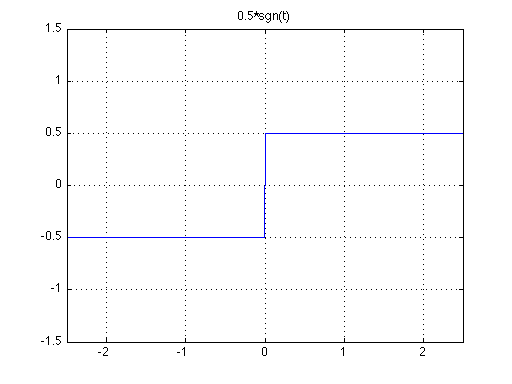
Figure 1. The Step Function u(t) [left] and 0.5*sgn(t) [right].
|
The reason we plot one half of the signum function in Figure 1, is that we can see that the unit step function
and the signum function are the same, just offset by 0.5 from each other in amplitude. For the functions in Figure 1, note that they have the same derivative, which is the dirac-delta impulse:
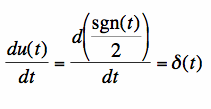 [3] [3]To obtain the Fourier Transform for the signum function, we will use the results of equation [3], the integration property of Fourier Transforms, and the the fourier transform of the impulse. The integral of the signum function is zero:
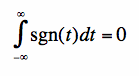 [5] [5]The Fourier Transform of the signum function can be easily found:
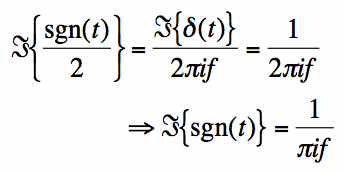 [6] [6]The average value of the unit step function is not zero, so the integration property is slightly more difficult to apply. Note that the following equation is true:
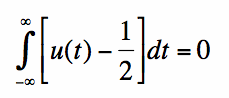 [7] [7]Hence, the d.c. term is c=0.5, and we can apply the integration property of the Fourier Transform, which gives us the end result:
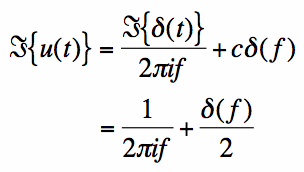 [8] [8]The integration property makes the Fourier Transforms of these functions simple to obtain, because we know the Fourier Transform of their derivatives.
|
Next: One and Two Sided Decaying Exponentials