Fourier Transformation

In some intellectual circles, Fourier Transforms are discussed using the term Fourier Transformation. This isn't unique or different from a Fourier Transform, and is seldom used. However, if you want the term Fourier Transformation defined, then this is the right place. If you are interested in learning about the Fourier Transform in detail, check out The Fourier Transform homepage. A Fourier Transformation is the process by which a Fourier Transform is taken. Typically, a Fourier Transform refers to a Fourier Transform pair, or the Fourier Transformation of a specific function. Fourier Transformation refers to the act of determining a functions Fourier Transform. 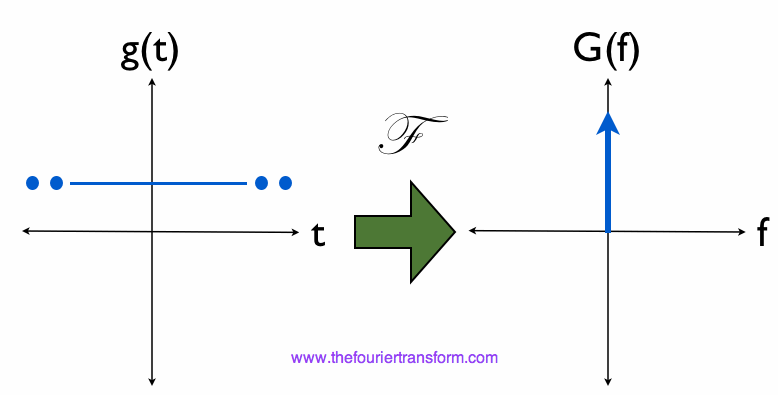Let's do a quick example. The constant function g(t) undergoes the Fourier Transformation to produce the dirac-delta function G(f), as shown in Figure 1: Figure 1. The Fourier Transformation of a Constant Function. If you are interested in really understanding the Fourier Transform, I encourage you to start with The Fourier Transform homepage, which goes through it all.