Far Field Radiation from Electric Current
The world of electromagnetics and radiation is governed by
Maxwell's Equations, a set of
complicated vector differential equations for determining Electric and Magnetic fields. On this page, we
are interested in determining the fields radiated by electric currents flowing on a surface. Specifically,
we want to know the Electric and Magnetic fields far from the source currents.
This problem has application in antennas, particularly
with determining the radiation patterns of
horn antennas. In addition,
determining the fields radiated from electric currents is useful in scattering applications, with the
most prevalent example being RCS (radar cross section).
[This page will require a good understanding of
spherical coordinates].
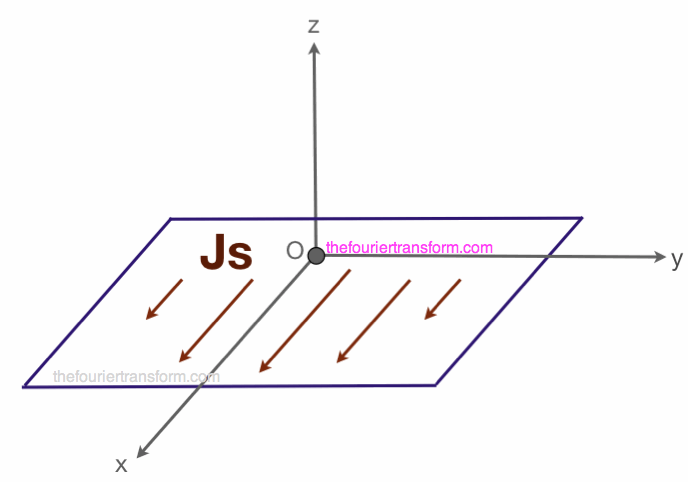
Consider a conductive surface (i.e. metal), enclosed within the purple boundary as shown in Figure 1. There
is an electric current, written by the vector Js, flowing on the surface as shown. We are intersted in the radiated
fields far from the surface.
Figure 1. An Electric Current (written with the vector Js) flows on a Surface.
We will write the radiated electric fields as the vector E in spherical coordinates:
Note that the radial component of the E-field (the field pointing in the direction of propagation) will always be zero
for radiated fields:
Before we determine the radiated fields from the full surface, let's note what the radiated fields are from
very small surface section. The radiated Electric Fields (E) from a very small section of the surface is given
by:
In Equation [2], R is the distance from the source point to the observation point (i.e., where we are measuring the
Electric Fields at),
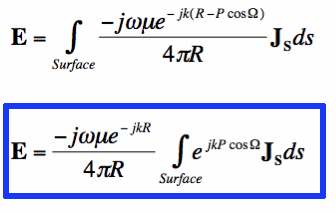
Now, to find the radiated fields from an area of surface current, we must simply sum up all the individual
small sections - that is, use integration:
To do this exactly, we would need to choose an observation point, and then
calculate R for each section of the surface to the observation point. This would make the integration
very difficult. Just as in the diffraction
section, we will make some approximations.
Recall that we are interested in the far-field radiation. This means the radiation far from the source current.
Since the function 1/R is slowly varying for large values of R, we can approximate this as a constant
for the entire surface, and pull it out of the integral in Equation [3].
This approximation should be understood - if you disagree, take the time to make sure it makes sense.
The term R also occurs in the exponential in Equation [3]. However, it is not ok to treat this as constant, because
the exponential is multiplied by the wavenumber, and is not necessarily a slowly varying function across the surface.
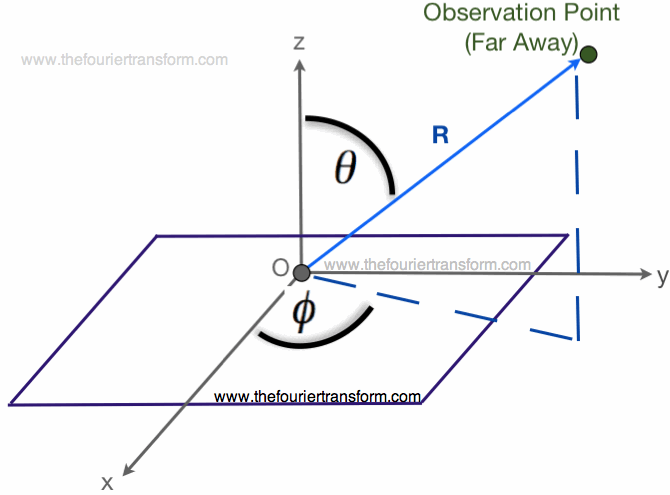
To make a proper approximation, let's walk through some geometry. First, assume we are interested in the fields
at some arbitrary point far from the surface. This point is defined in terms of R, theta and phi:
Figure 2. An arbitrary observation point, far from the surface. The point is defined in terms
of R, theta and phi.
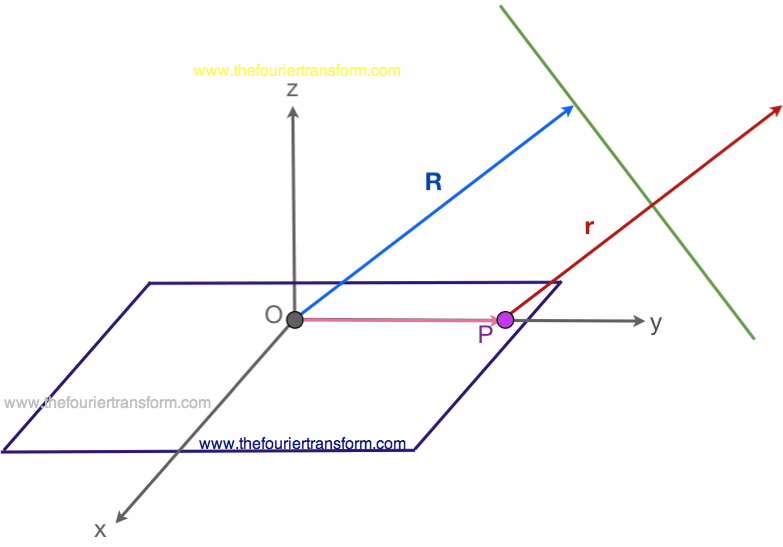
Now consider an arbitrary point on the surface, P, as shown in Figure 3:
Defining the Problem: Electric Current Flowing on a Surface
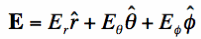
[Equation 1]
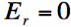 .
.
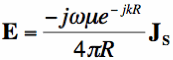
[Equation 2]
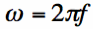 is the angular frequency in radians/second,
is the angular frequency in radians/second,
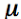 is the
permeability of free space (a constant), and
k is the wavenumber. We also
use the convention of j being the square root of negative 1, the imaginary number (which gives us phase information).
Note that in Equation [2], the radially-directed E-fields (in the
is the
permeability of free space (a constant), and
k is the wavenumber. We also
use the convention of j being the square root of negative 1, the imaginary number (which gives us phase information).
Note that in Equation [2], the radially-directed E-fields (in the 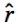 direction) are zero.
direction) are zero.
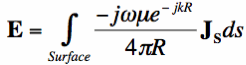
[Equation 3]
|
In Figure 3, I have drawn the vectors R and r with the same magnitude (size) and direction. Because the observation point (where we want to calculate the E-fields) is very far away (and much larger than the surface where the electric currents flow), these two vectors will be approximately parallel. However, because they travel different distances, one ray will arrive quicker than the other (a shorter distance).
The green line in Figure 3 is perpendicular to the
|
|
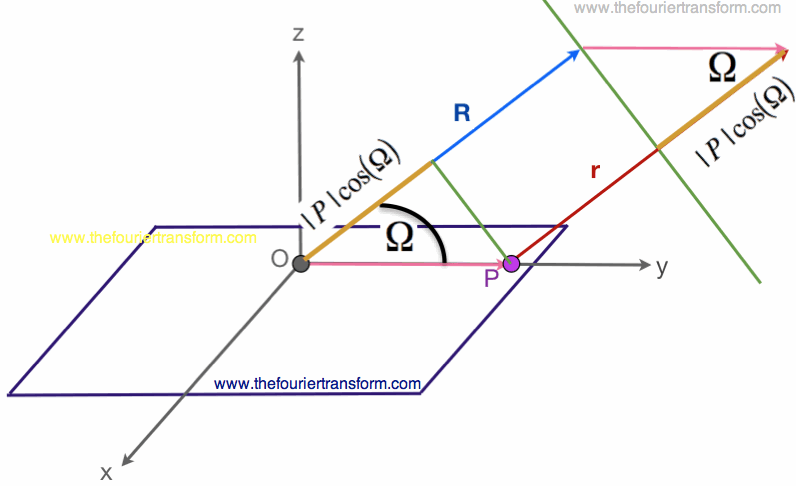
Figure 4. Graphical illustration of determining the relative phase between the two vectors.
In Figure 4, we define
By observing the geometrical relationships in Figure 4, you see that the vector r
travels a longer distance than the vector r, where the extra distance is equal to
Therefore, we need to subtract out this phase from the complex exponential in Equation [3]. That is, for an arbitrary point on the surface, the phase will be modified as:
In Equation [4], R is now a constant, which is equal to the distance between the origin of our coordinate system and the observation point. We can now use Equation [4] in Equation [3] to determine the far fields from the electric surface currents:
In Equation [5], P represents the distance of an arbitrary point on the surface (that we are integrating over) and the origin. The result in Equation [5] may not look helpful or simplified. But as we will see, the radiated far fields from a surface current are equal to the Fourier Transform of that current!
Example
Let's look at an example where the surface is a region in the x-y plane, where electric current is flowing. We can use Equation [5] to determine the radiated fields far from the source. Take the surface in Figure 1 (in the x-y plane), and let's assume the surface current Js is given by:
Equation [6] is that of a surface current that travels in the +x-direction, with a constant magnitude (Jo) everywhere over a square region of width a in the x-direction and length b in the y-direction. We now need to evaluate Equation [5] to with this surface current function to determine the radiated fields. We first note that dS = dx dy, since we are integrating over a flat region in the x-y plane:
Now we want simplify the exponential. Note that
If we first define the two dimensional Fourier Transform as:
We can now insert Equation [8] into Equation [7], and we see the Fourier Transform emerge:
In addition, if we rewrite our surface current as the product of two functions of one variable:
Then we are left with two one dimensional Fourier Transforms:
In Equation [12], the standard one-dimensional fourier transform definition is used:
From Equations [12] and [13] and the solution for the Fourier Transform of a box function, we can compute the integrals in [12]:
Note that in Equation [14], sinc(-x)=sinc(x), so we can drop the minus signs in the sinc() functions.
There is one final step before we can evaluate the radiated fields. We were able to pull out the
constant unit vector in the x-direction,
Finally, by incorporating Equations [12], [14], [15] into Equation [5], we have the solution:
Since the selected observation point was arbitrary, we found the radiated fields for all directions from this surface electric current distribution! Also, having this description of the electric field in vector form also tells us the polarization of the radiated fields. To cement the example, let's look at the normalized (forgetting the terms in front of the sinc functions) magnitude of E:
This function is also known as the radiation pattern, if we view the surface current as an antenna.
We can plot the fields of Equation [17] for
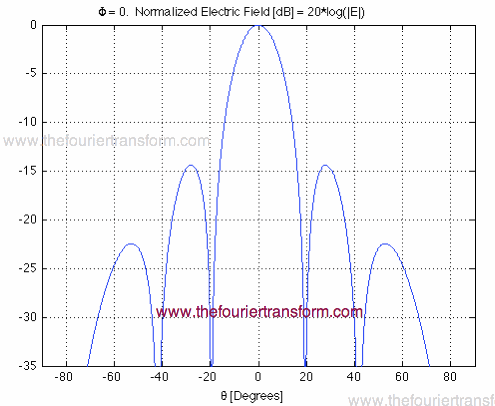
Figure 5. Radiated Electric Fields as a function of theta, for
Horn AntennasWe can also use this technique to calculate the radiation pattern for horn antenna. Horn antennas are basically apertures with an electric field across them, which gives rise to the radiation. Now, we can model an electric field as a "magnetic surface current" Ms:
In [18],
In Equation [19],
Radar Cross Section - RCSRadar works by transmitting an electromagnetic wave from an antenna. The wave then bounces off some object, and the returned energy is measured. The amount of energy returned is a function of the radar cross section of the object. If we can estimate the fields radiated by an antenna, we can estimate the surface electric current induced on an object (such as an airplane). From these fields, we can use Equation [5] (which we now know how to solve) to determine the reflected power as a function of angle. In this way, the radar cross section of objects can be determined, particularly as they fly across the sky. This application is common in military defense programs. If you managed to stay with me through this whole page, I am very impressed. I hope you enjoyed the ride as much as I did.
Fourier Transform Applications The Fourier Transform (Home)
If you are reading this page anywhere except on thefouriertransform.com, this is stolen work. This page on the application of Fourier Transforms to radiation due to surface currents is copyrighted. No portion can be reprinted except by permission from the author. Copyright thefouriertransform.com, 2010-2012. See also VSWR. |
 as the angle between the vectors r and R.
By using some geometry, we see that the gold line has a distance equal
to
as the angle between the vectors r and R.
By using some geometry, we see that the gold line has a distance equal
to 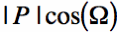 (where |P| is the distance from the origin [O] to the point [P]).
(where |P| is the distance from the origin [O] to the point [P]).
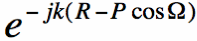
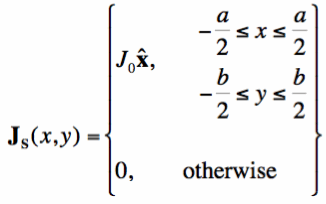
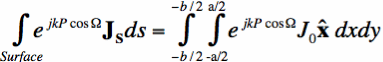
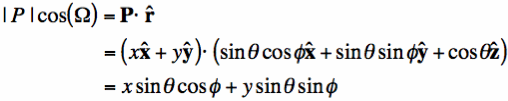
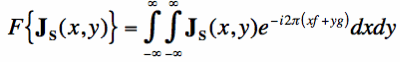
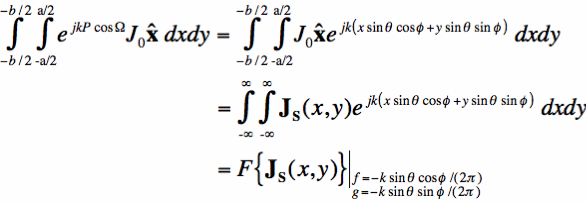
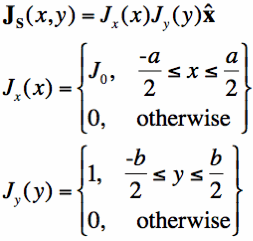
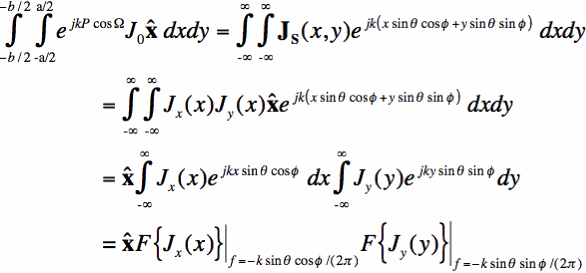
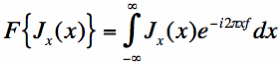
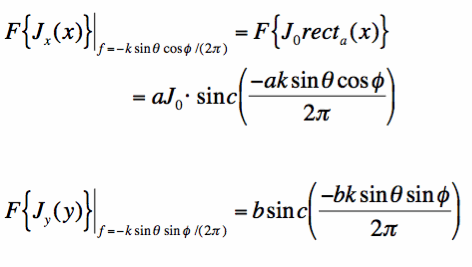
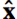 .
We must convert the
.
We must convert the  and
and  vectors (unit vector in the theta and phi
directions). This is a simple transformation, but we need to do it because the
vectors (unit vector in the theta and phi
directions). This is a simple transformation, but we need to do it because the 
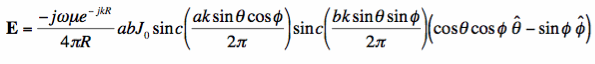
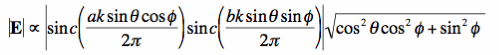
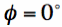 versus theta,
for a=b=
versus theta,
for a=b=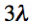 .
Using
.
Using 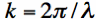 , we can plot the magnitude of the electric field:
, we can plot the magnitude of the electric field: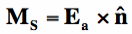
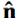 is a unit vector perpendicular to the surface. The far field
results can then be calculated
using [18] in place of Js, and replacing the electric field with the
is a unit vector perpendicular to the surface. The far field
results can then be calculated
using [18] in place of Js, and replacing the electric field with the
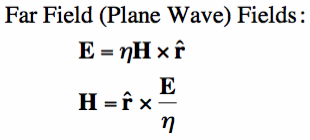
 is a constant (about 377 Ohms), known
as the
is a constant (about 377 Ohms), known
as the