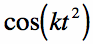The Fourier Transform of the Quadratic Sinusoids

The Quadratic Cosine Function

Are you interested in the sinusoidal functions with a quadratically varying phase? This is the right page. The function is a cosine or sine function with an argument of t-squared instead of t. The cosine version is given in Equation [1], and plotted in Figure 1 below:

		[Equation 1]

Figure 1. Plot of Quadratic-Cosine for k=1.

The Fourier Transform for the cos(t^2) function can be found fairly easily using the Fourier Transform for the Complex Gaussian. We begin by rewriting the cosine function using Euler's formula:

		[Equation 2]

Assume k is positive. If k is negative, the result will still be the same, which you can work through [note that the cos(-x)=cos(x)]. If k is zero, then we have a constant and not a quadratically-varying sinusoid. The Fourier Transform can be found since we know the Fourier Transform of the complex Gaussian. The terms in Equation [2] can have the Fourier Transform taken:

		[Equation 3]

The other term in Equation [2] can be found by using the Fourier Transform of the Complex Gaussian for the case of a negative real constant, simply by manipulating the signs:

		[Equation 4]

The end result can then be obtained:

		[Equation 5]

If k is negative, the Fourier Transform should not change, because cos(kt^2) is an even function. Hence, the general result is:

		[Equation 6]

This function is plotted in Figure 2:

Figure 2. Plot of Fourier Transform of Quadratic-Cosine [Eq 6] for k=1.

The Quadratic Sine Function

		[Equation 7]

Figure 3. Plot of Quadratic-Sine for k=1.

The Fourier Transform of this function can be found using the same technique. That is re-writing the sine function as:

		[Equation 8]

For positive k, we can work through the above math as before and get the result:

		[Equation 9]

To get the general result (including negative k values), recall that

sin(-t)=-sin(t). The end result:

		[Equation 10]

Equation [10] is plotted in Figure 4 for k=1:

Figure 4. Plot of Fourier Transform of Quadratic Sine (Eq [10]) for k=1.