Fourier Transform Applied to Partial Differential Equations
As an example of solving Partial Differential Equations, we will take a look at the classic
problem of heat flow on an infinite rod. That is, essentially
we are interested in the temperature of the rod; we'll call the temperature as a function
of position (x) and time (t) by G(x, t). Side Note: solving heat flow on a circular ring is
actually the original motivation for Fourier Series and Fourier Transforms by Fourier!
Now, heat flow on a rod is governed by the partial differential equation:
A couple of things to note in equation [1]:
We will introduce an initial condition and look to solve for the heat function g(x,t) for
all values of t>0. That is, suppose we know the temperature distribution on the rod
for all x at t=0:
We call the intial temperature distribution h(x). Our goal now is to solve the PDE in Equation [1]
subject to the condition in Equation [2].
To accomplish this, we will use (you guessed it) the Fourier Transform. To start, let's take the
Fourier Transform of Equation [1] with respect to x. That is, we will assume x is
the variable and hold t constant. First, we will take the Fourier Transform of the right
hand side of Equation [1]:
Note that in Equation [3], we are more or less treating t as a constant. The Fourier Transform
is over the x-dependence of the function. We also define G(f,t) as the Fourier Transform with
respect to x of g(x,t).
The next step is to take the Fourier Transform (again, with respect to x)
of the left hand side of equation [1]. To do this, we'll
make use of the linearity of the derivative and integration operators (which enables us to exchange their order):
Now that we have the full Fourier Transform of Equation [1], we set Equation [3] equal to Equation [4]:
Equation [5] represents a simple Ordinary Differential Equation in the variable t; the function
we seek is G(f,t). Using elementary differential equation methods, we obtain:
The function G(f, 0) represents the initial condition for the differential Equation in [5]. We also
know that G(f, 0) is just the Fourier Transform with respect to x of g(x, 0); and
from Equation [2] we know that g(x, 0) is just h(x). Hence, we re-write the initial condition
as the Fourier Transform of h(x), and call it H(f):
Recall that the goal here is to get g(x, t). We can obtain this by taking the inverse Fourier Transform (with
respect to x) of Equation [7]. Also, note that Equation [7] represents the product of two functions: H(f)
and the Gaussian Function.
As a result, hopefully you recognize that
a convolution will be coming
in the x domain.
Before that, we will take the inverse Fourier Transform of the Gaussian in Equation [7] (if you want
to see how this is derived, see here):
Equation [8] can be used to take the inverse Fourier Transform of Equation [7]:
The result in Equation [9] represents the general solution of Equation [1], subject to the condition
of Equation [2]. The result, in essence, represents how the initial heat distribution smooths itself
out over time. That is, as t approaches 0, g(x,t) approaches h(x). This is because the Gaussian function
becomes very sharp and approximates an impulse function.
As time increases, the integration of Equation [9] represents a "smoothing out" or averaging of the initial
temperature distribution h(x). This equation dictates precisely how heat spreads out on a rod.
On the previous page on the
Fourier Transform applied to differential equations,
we looked at the solution to ordinary differential equations. On this page, we'll
examine using the Fourier Transform to solve partial differential equations (known as PDEs), which are essentially multi-variable
functions within differential equations of two or more variables.
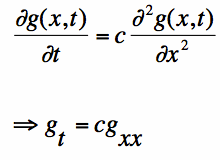
[Equation 1]
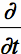 represents the partial derivative with respect to time.
That is, the derivative is taken with respect to t while treating x as a constant.
The same goes for the partial derivative with respect to x (t is held constant).
represents the partial derivative with respect to time.
That is, the derivative is taken with respect to t while treating x as a constant.
The same goes for the partial derivative with respect to x (t is held constant).
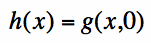
[Equation 2]
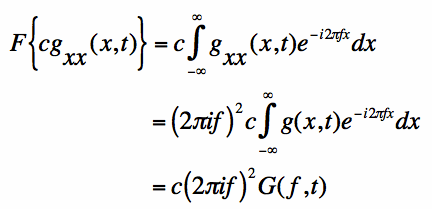
[Equation 3]
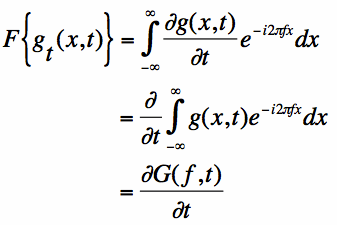
[Equation 4]
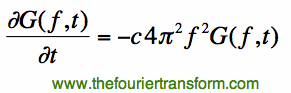
[Equation 5]
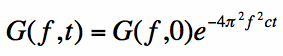
[Equation 6]
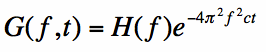
[Equation 7]
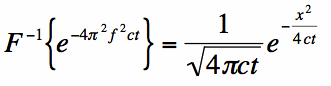
[Equation 8]
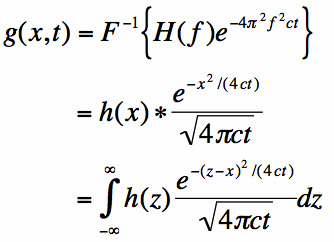
[Equation 9]
Previous: Ordinary Differential Equations
Fourier Transform Applications
The Fourier Transform (Home)