Diffraction Through an Aperture
Now that we know a little bit about light and plane waves, we'll look at how they behave when
incident upon an aperture. Suppose a plan wave of light (with E-field polarized in the +x-direction, as before)
is incident upon an aperture, as shown in Figure 1.
Note that the aperture in the aperture plane is just made up of any material that blocks light, and can support
a slit or hole in it to pass the light.
Figure 1. A Plane Wave of Light is Incident Upon an Aperture.
In Figure 1, we have a plane wave travelling in the +z-direction, emitted by a source. It impinges upon
the aperture. The distances R1 and R2 are large enough such that the fields will behave as plane waves
(which for a small light source is easily satisfied at a distance of a couple meters).
The question is: What is the electric field on the image plane, a distance R2 further down the z-axis?
To figure this out, we again assume the E-field is written as:
For a coordinate system, let's take the center of the aperture opening to be the origin. Then Equation [1],
the field incident upon the aperture, reduces to:
The important thing about equation [2] is to note that the E-field is constant across the aperture.
That is, the field does not vary as a function of x. Hence, this aperture is said to be uniformly illuminated.
The fields on the image plane must arise soley from the fields on the aperture: everywhere else in the aperture plane
is blacked out.
To find the fields on the image plane, let's assume we are looking at the fields on the image plane at a specific
point Z, due to the field as a specific point X as shown
in Figure 2:
Figure 2. Determining the Field at Position Z due to Field at Position X.
Figure 2 is key to the derivation, so I will take it slow. First, X is some arbitrary point in the aperture. We are
looking for the fields at some point Z in the image plane. The coordinate system is set up such that x=0, z=0
is the center of our aperture.
Now, we define R0 as the distance between our origin and the point Z. The vector
from the origin to Z makes an angle
Figure 3. Enlargement of Figure 2 to understand where R0-Xsin(
Even though the approximation is not exact, since we are assuming we are in the far field, the rays from position X
and from the origin should be approximately parallel. Hence, the distance used is valid. If this isn't clear or you don't
believe me, take some time to work through the math and prove it to yourself. The distance between X and Z
then is:
Now, if we want to know the total field at point Z, then we need to add together every point in the aperture.
That is, we need to integrate across the aperture to get the field at point Z. To get this, we'll have to
know a little more physics. Specifically, the fields from a point source can be modeled as:
That is, equation [3] states that the fields from a point source of frequency f
die off in magnitude like 1/r (where r is the distance
from the point), and the phase varies similar to a plane wave.
Recall that we are interested in integrating every point in the aperture to determine
the fields at Z. Let's integrate across the aperture, using the point source equation [4],
and the distance for each point X given in equation [3]:
Note that we write E(Z) even though Z does not appear on the right hand side; the reason is that
Z can be determined from
Figure 4. The Aperture Function for a Slit of Length 2.
Back to Equation [5]: this looks somewhat intimidating, but it will simplify nicely. First,
we can make the simplification:
Equation [6] is valid because for large values of R0, the function 1/R changes very slowly. Physically,
this means that far from the source, the amplitude does not change very rapidly. Therefore, if R0>>X,
this approximation introduces negligible error.
Now, we might be tempted to simplify the phase term in Equation [5] by also dropping the Xsin(
Substituting Equation [6] into Equation [5], and performing some algebra, we get:
The term on the outside of the integral in the second line of Equation [7] is just a constant,
so we will replace it with the constant C. In addition, we will introduce the
variable q, defined by:
Using Equation [8] in Equation [7], we get:
Equation [9] states that the fields on the image plane are the Fourier Transform of the aperture
function A(X)!
Hence, light passing through a slit, under the right conditions (narrow bandwidth, far field) will
produce the Fourier Transform of the aperture (slits) plane. This is pretty cool. Equation [9] is
the main result of the last two pages, so hopefully you have a good idea where it comes from
and the assumptions involved. In the next section,
we'll look at the results for different apertures, and see the Fourier Transform show up in the real world.

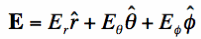
[Equation 1]

[Equation 2]

 with the +z-axis. We now
make the assumption that R0>>X. Using this approximation,
then the distance between our point X and Z is given
by R0-Xsin(
with the +z-axis. We now
make the assumption that R0>>X. Using this approximation,
then the distance between our point X and Z is given
by R0-Xsin( ). This approximation is realistic since we can simply back up our image
plane such that the distance is much much larger than our aperture. To further understand Figure 2,
observe Figure 3, which is a zoomed in view of Figure 2 and helps to clarify where the R0-Xsin(
). This approximation is realistic since we can simply back up our image
plane such that the distance is much much larger than our aperture. To further understand Figure 2,
observe Figure 3, which is a zoomed in view of Figure 2 and helps to clarify where the R0-Xsin( )
term comes from.
)
term comes from.

 ) comes from.
) comes from.

[Equation 3]
More Physics

[Equation 4]

[Equation 5]
 . The function A(X) defines the aperture. That is,
A(X)=1 where the aperture is open (the slits), and A(X)=0 in the region where the material on the aperture
plane blocks the light. For a slit centered at X=0 and of width 2, the function A(X) will be:
. The function A(X) defines the aperture. That is,
A(X)=1 where the aperture is open (the slits), and A(X)=0 in the region where the material on the aperture
plane blocks the light. For a slit centered at X=0 and of width 2, the function A(X) will be:

[Equation 6]
 ).
However, the phase function does vary rapidly (even for large R, since the complex exponential function is periodic).
Therefore, we cannot use the same simplification we use for the amplitude (in equation [6]).
).
However, the phase function does vary rapidly (even for large R, since the complex exponential function is periodic).
Therefore, we cannot use the same simplification we use for the amplitude (in equation [6]).

[Equation 7]

[Equation 8]

[Equation 9]
Next: Fourier Transforms of Apertures
Fourier Transform Applications
The Fourier Transform (Home)